INTRODUCCION
Una matriz es un arreglo rectangular de números en renglones y columnas. Las dimensiones de una matriz indican el número de renglones y columnas de la matriz en ese orden. Como la matriz A tiene 2 renglones y 3 columnas, se le llama una matriz de 2 × 3 2\times 3 2×3 .
DEFINICION
Una matriz es un conjunto de números ordenados en filas y columnas.
Las matrices tienen por nombre una letra mayúscula y sus elementos se encierran entre dos paréntesis (o dos corchetes)
Ejemplo de matriz:

Decimos que una matriz es de orden ![]() (o de dimensión
(o de dimensión ![]() ) cuando tiene
) cuando tiene ![]() filas y
filas y ![]() columnas.
columnas.
La matriz  es de orden
es de orden ![]() (tiene 2 filas y 3 columnas)
(tiene 2 filas y 3 columnas)
Una matriz de orden ![]() se expresa de forma genérica:
se expresa de forma genérica:
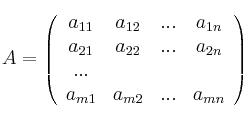
donde el elemento ![]() denota que está en la fila
denota que está en la fila ![]() y en la columna
y en la columna ![]()
En la matriz  el elemento
el elemento ![]() (fila 2 , columna 1) vale
(fila 2 , columna 1) vale ![]() .
.
Todos los elementos de la matriz A:
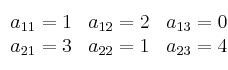
NOTACION
La notación común para las matrices utiliza una letra negrita para la matriz, e identifica sus elementos en términos de filas y columnas de la matriz. Teniendo en cuenta que una matriz es una formación rectangular, podemos hablar de la matriz m x n (se lee matriz de m por n) como la que tiene m filas y n columnas.
ARITMETICA MATRICIAL (Suma y Multiplicación)







No hay comentarios.:
Publicar un comentario